Torres de Hanoi

Introducción

Las Torres de Hanói es un rompecabezas o juego matemático inventado en 1883 por el matemático francés Édouard Lucas.

Este juego es un interesante ejemplo de diferentes conceptos tanto matemáticos como informáticos:

Reglas del juego

El juego consta de cierto número de discos perforados de radio creciente que se apilan insertándose en tres postes fijados a un tablero. El objetivo del juego es trasladar toda la pila de discos de uno a otro de los postes moviendo los discos de uno en uno de un poste a otro y sin colocar un disco más grande encima de otro más pequeño.

Demostración por inducción de la existencia de la solución

Es fácil demostrar por inducción que el juego tiene solución:

Supóngase que ya se sabe cómo mover una pila de n discos de uno de los postres a otro. Se puede demostrar que, si eso es posible, se pueden mover n+1 discos de un poste a otro. Para ello bastaría tomar los n discos superiores de la pila de n+1 discos y moverlos a uno de los postes vacíos, cosa que suponemos que sabemos hacer; luego se movería el disco restante al otro poste vacío y volveríamos a mover los n discos del poste donde han quedado al poste que solo tiene el disco mayor.
Para completar la demostración por inducción tenemos que demostrar que sabemos mover un número de discos inicial, así el razonamiento anterior podrá arrancar. Pero es evidente que sabemos mover un solo disco de un postre a otro, por lo que, aplicando el método anterior, sabremos mover 2, luego 3 y todos los que queramos.

Programación recursiva

Si se quiere programar el juego, El razonamiento anterior da pie a una solución recursiva del problema:

Construiremos una función (método) para mover n discos de un poste a otro. En primer lugar, esa función se llamará a sí misma para mover n-1 discos a uno de los postes libres, luego moveremos el disco restante al otro poste libre y volveremos a llamar a la propia función para mover los n-1 discos de donde han quedado al poste donde se encuentra el disco restante. La condición de salida de esa función será que solo haya que mover un disco.

Crecimiento exponencial de la complejidad

De los apartados anteriores se puede deducir que la complejidad del problema crece exponencialmente con el número de discos de la torre, ya que para mover la pila de n discos de un poste a otro hay que mover dos veces una torre de n-1 discos por lo que el número de movimientos cada vez que se añade un disco a la torre se multiplica por 2. A partir de esto, se puede demostrar que el número mínimo de movimientos necesarios para trasladar una torre de n discos de un poste a otro es 2ⁿ-1.

La leyenda del inventor del ajedrez

El concepto de crecimiento exponencial enlaza con la vieja leyenda del inventor del ajedrez.

Dice esa leyenda que el rey de la India quiso recompensar al inventor del ajedrez como él quisiera por haber ideado un juego tan interesante. El inventor reflexionó y pidió un grano de trigo por la primera casilla del tablero, 2 por la segunda, 4 por la tercera y así sucesivamente, multiplicando por 2 el número de granos de la casilla anterior, hasta acabar con todas las casillas del tablero. Al rey le pareció justo y accedió sin darse cuenta de la cantidad de trigo que ello suponía.

Se deja como ejercicio para el lector calcular las toneladas de trigo necesarias para pagar el premio suponiendo que cada grano de trigo pesa 30 mg. De forma parecida también se puede calcular el tiempo mínimo necesario para mover una torre de Hanói de 64 discos de un poste a otro suponiendo que cada movimiento emplea un segundo.

Simulación

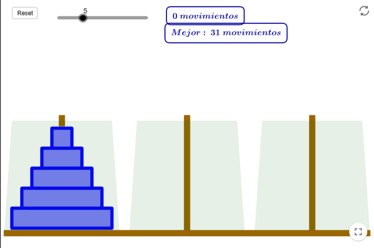
Pinchando en la siguiente imagen puede encontrarse una página web que simula el juego de las Torres de Hanói

Referencias

Pieza cedida por Javier Bastida Ibáñez